• Éditer la page
• Historique
• Rechercher
• Imprimer

Manuel SELLIER

Fonction au club : Membre
Né le : 23/05/1980
Catégorie : Ufolep 1ere catégorie
Profil cycliste : Enorme rouleur. A tendance à apprécier le goudron, à regarder tout sous l’angle de son wattmètre et à être plus obnubilé par son coefficient aérodynamique que par sa forme physique !
Titres de gloire : Dès sa première saison, en 2006, Manu a quasiment tout gagné, à commencer par sa première course, en 3e catégorie, puis sa deuxième en 2ème catégorie, et rebelotte jusqu'à sa montée express en 1ère. Il a obtenu, depuis, de remarquables résultats, tels cette 3eme place au national CLM UFOLEP 2007, sa victoire au Tour de Guadeloupe 2008 ou encore sa 1ère place au Tour du Lac de Paladru CLM en 2009, sans compter ses nombreuses victoires en 1ere catégorie. En 2010, malgré un entraînement en dent de scie, Manu a glané un formidable succès en solitaire sur la dernière étape du Tour des Grands Ducs. Il est vice-champion régional du CLM en 2011, et 3ème du championnat national 2014 de CLM en catégorie 30-39 ans. Il renoue avec la victoire en 2013 à Rives et à Cras, en 2014 au Triptyque du Fontanil et devient vice-champion de CLM en catégorie 30/39 ans.

Quelques photos

Analyse de la performance cycliste – Modèle de temps de parcours sur un CLM

Introduction

A première vue on pourrait croire qu’il est presque aussi difficile de répondre à la question « qu’est ce qui fait avancer le cycliste » qu’à la question « qu’est-ce qui fait avancer le monde ? ». Pourtant, en y regardant de plus près, il semblerait qu’il soit plus facile de donner des éléments de réponse à la première question qu’à la deuxième. Ca ne veut pas dire que la deuxième question ne soit pas intéressante ou qu’il ne soit pas possible d’en dire quelques mots, mais bon, ce n’est pas l’objet du présent article !

Tout d’abord, situons les forces en présence. Car ce sont bien elles qui freinent le cycliste. En effet, sans elles, même une force de propulsion infime suffirait à donner une vitesse infinie au cycliste. Quand le frein est la pente d’un col, on comprend bien que les qualités premières d’un bon cycliste seront sa légèreté et sa force physique (disons sa puissance). Mais quand le frein est l’air et le roulement des roues (cas d’une route plate), les critères de performances deviennent moins évidents. Le but de cet article est précisément de pouvoir répondre à des questions peu évidentes du style « Faut-il perdre du poids pour bien marcher dans un chrono vallonné ? », « Est-ce que ça vaut le coup de s’acheter un vélo de chrono en carbone ? », « quel est le gain d’une lenticulaire ? », « Faut-il forcer dans les bosses ou dans les descentes ? », «Quel gain ai-je à utiliser des boyaux ? » etc.…

Répondre à ces questions semble de prime abord bien compliqué. Pourtant, en exprimant clairement les forces s’appliquant sur le cycliste, beaucoup de choses s’éclaircissent.

Forces en présence

Comme disait mon prof de prépa, un bon schéma vaut toutes les explications du monde :

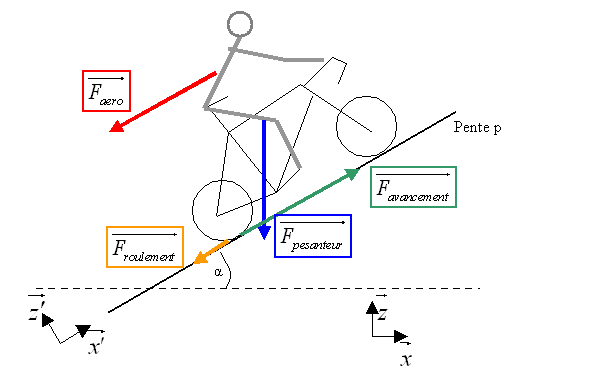
Regardons donc de près les forces en présence :

Force de la pesanteur (ou Poids) : véritable ennemie du cycliste dans les cols, la force de la pesanteur est égale à :

Avec m la masse du cycliste avec son vélo et g l’accélération de la pesanteur (égale à 9,81 m/s).

La force de la pesanteur peut-être exprimée de la manière suivante (en prenant comme définition de la pente p, le sinus de l’angle α de la route par rapport à l’horizontale) :

Force de frottement dans l’air : cette force est le principal frein du cycliste lorsque celui-ci roule sur le plat ou en descente. Elle peut s’exprimer sous la forme suivante :

Avec Cd le coefficient de traînée, A la surface frontale du cycliste et de son vélo, ρ la densité de l’air (typiquement 1,2 kg/m³ à l’altitude 0), et v la vitesse du cycliste par rapport au vent (c’est la vitesse du cycliste par rapport au sol lorsque la vitesse du vent est nulle). . Le produit Cd.A varie typiquement entre 0,2m² pour les meilleurs coureurs pro en position de CLM (Zabrisky par exemple !) et 0,7m² pour le cycliste « Velib » droit sur son vélo

Force de roulement :

Avec C_rr le coefficient de roulement des pneus. Ce coefficient vaut typiquement 0,005 pour des pneus standard roulant sur une route correcte

Force d’avancement :

Cette force résulte directement des forces qu’applique le cycliste sur les pédales. Etant donné que l’effort est proportionnel à la puissance (puissance = force sur les pédales*vélocité), il est préférable d’exprimer la force d’avancement en fonction de la puissance pour être plus parlant. On sait que la puissance est la dérivée par rapport au temps de l’énergie fournie par le cycliste (soit la dérivée du travail de la force d’avancement) :

D’où

Principe fondamental de la dynamique :

Selon le principe fondamental de la dynamique :

Selon l’axe x’, cela donne :

Ce qui est équivalent à

qui est équivalent à (1)

A vitesse constante est nul d'où

(2)

Cette relation permet d’exprimer simplement la puissance à fournir pour aller à une vitesse donnée. Nous noterons que la puissance à fournir par le cycliste (l’intensité de son effort en quelque sorte) augmente pour une partie avec le cube de la vitesse ! Cela veut dire qu’il faut donc dépenser 8 fois plus d’énergie pour seulement doubler sa vitesse sur le plat ou en descente (lorsque le terme est prédominant) alors qu’il faut seulement multiplier par deux l’intensité de son effort pour doubler sa vitesse en côte (lorsque domine). Cela explique pourquoi il est beaucoup plus rentable de forcer dans les montées plutôt que dans les descentes.

Application numérique : Quelle puissance faut-il typiquement développer pour rouler à 45km/h sur le plat ?

Un bon cycliste aura un CdA de 0,26 en position CLM. En prenant 0,005 pour le coefficient de roulement des pneus, 80kg pour le poids homme+machine, la puissance à développer sera typiquement de P=0,5*1,2*0,26*(45/3,6)^3 + 80*9,81*0,05*(45/3,6)=305+49=354W !

Il faudra donc que notre cycliste développe une puissance de 354W pour rouler à 45 km/h (plus de 300W pour lutter contre l’air et près de 50W pour lutter contre le coefficient de roulement des pneus)

Méthode pour calculer le temps d’un CLM sous Excel à partir des données POLAR :

Avec des cardiofréquencemètres de type POLAR, nous pouvons enregistrer de manière discrète les données d’altitude et de distance sur un parcours de CLM par exemple.

Soit A_n, d_n respectivement l’altitude et la distance à la n^ième mesure

La pente peut alors être écrite de la manière suivante :

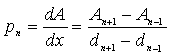
En définissant t_n, le temps pour effectuer le tronçon [d_n-1 ;d_n ] et v_n la vitesse sur ce même tronçon, on a :

et

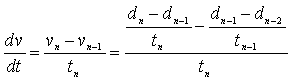
D’où, d’après (1), en notant P_n la puissance sur l’intervalle [d_n-1 ;d_n ]:

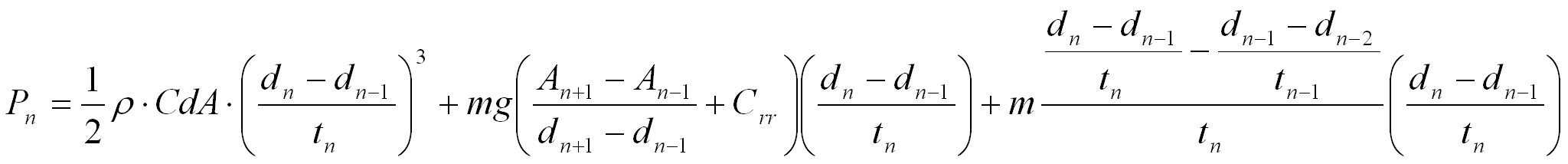(3)

On est donc capable d’exprimer la puissance P_n en fonction du temps mis à parcourir le tronçon en cours et celui d’avant (t_n, t_n-1), des paramètres du parcours (d_n+1, d_n, d_n-1, A_n+1, A_n-1) et des paramètres du cycliste/vélo (ρ, CdA, Crr,m).

Connaissant la puissance P_n capable de fournir le cycliste, on peut remonter au temps t_n pour parcourir le tronçon [d_n-1 ;d_n ]. Pour cela, il suffit de faire résoudre l’équation P_n=f(t_n) par le solveur Excel (goalseek). Ensuite, on n’a plus qu’à additionner les t_n pour retrouver le temps final :

Limites : Ce modèle n’est valable que sous certaines conditions :

• Pas de vent (bien qu’il soit facile de mettre un facteur correctif)

• Coefficient de roulement constant

• CdA constant. En d’autres termes les calculs ne sont valables que pour une position constante tout au long du parcours. Par ailleurs le CdA varie toujours un peu avec la vitesse à cause des roues.

• Pas de force de freinage (on ne sait pas modéliser cette force) ! Ceci est bien sûr assez limitant puisqu’il est rare de trouver des parcours de CLM où il n’y a pas besoin de freiner)

• Echantillonnage discret : le fait d’échantillonner les valeurs toutes les 5s a tendance à lisser les effets dus aux accélérations. L’impact de la modulation de puissance sur le temps de parcours du CLM est ainsi sûrement sous-estimé.